1. 기본 용어
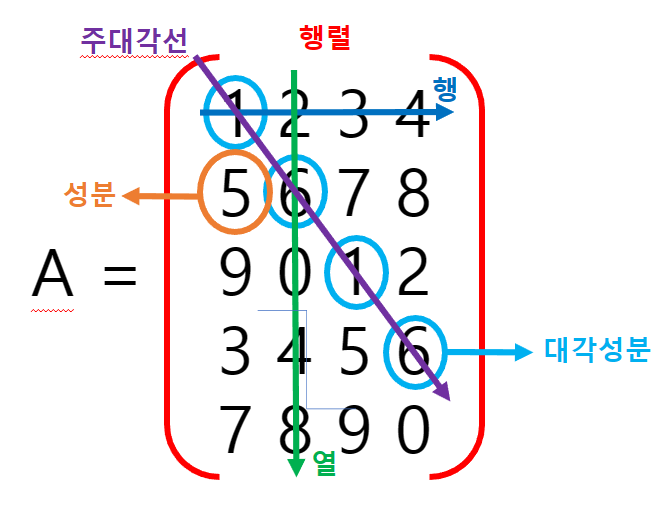
- 행렬: 직사각형 모양으로 배열된 일련의 숫자.
- 요소: 매트릭스에 배열된 요소
- 행: 행렬의 수평선
- 열: 행렬의 세로 행
- mxn 행렬: m 행과 n 열을 갖는 행렬
- 주 대각선: 행렬의 왼쪽 위 모서리와 오른쪽 아래 모서리를 구분하는 선입니다.
- 대각선 요소: 행 및 열 인덱스가 동일한 요소 – (1, 1), (2, 2) …
TMI: 2D 어레이 int arr(x)(y); x는 실제로 수직 길이 in임을 기억하십시오. 사실 “이전은 가로가 아니라 세로라고 왜 헷갈려?!” 세로 길이가 아니라 실제로 행의 수라고 불평했습니다!
2. 행렬의 종류
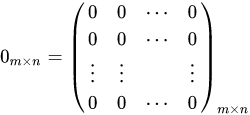
1) 영행렬 또는 영행렬: 모든 원소가 0인 행렬
2) 전치 행렬: 주어진 행렬의 행과 열을 바꿔서 얻은 행렬.
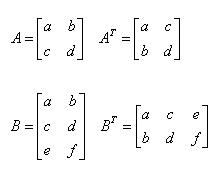
3) 대칭행렬: 행렬을 전치하면 원래 행렬과 같은 행렬이 된다.
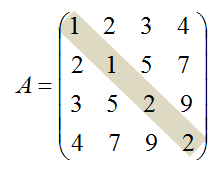
4) Skew-Symmetrix Matrix: 전치행렬이 덧셈 역행렬과 같은 행렬.
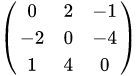
5) Square Matrix: 행과 열의 개수가 같은 행렬

6) 대각선 행렬: 대각선 요소를 제외한 모든 요소가 0인 정사각 행렬.

7) 항등 행렬: 모든 대각선 요소가 1이고 나머지 요소가 0인 정사각 행렬.
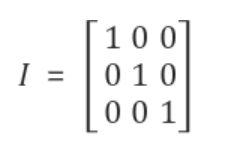
3. 행렬 연산
1) 행렬 덧셈과 뺄셈
일반적인 행렬 덧셈과 뺄셈은 매우 직관적이므로 덧셈과 뺄셈 방법을 알면 쉽게 기억할 수 있습니다. 덧셈과 뺄셈은 아래와 같이 같은 위치에 있는 성분을 단순히 더하거나 빼면 됩니다.
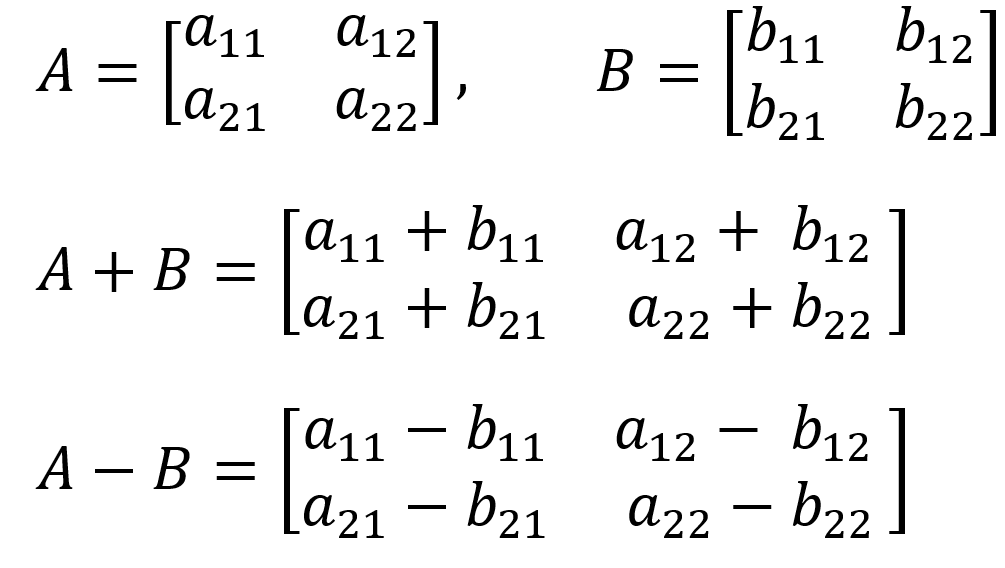
2) 행렬의 스칼라 곱셈
덧셈과 뺄셈보다 쉽습니다. 행렬의 모든 요소에 곱하려는 숫자를 곱하기만 하면 됩니다. 일정한 곱셈으로 생각하십시오. 더 이상 설명할 것이 없습니다.
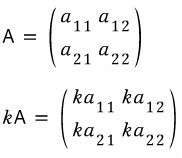
3) 행렬 곱셈
누군가가 주문을 두 번 불렀기 때문에 이 부분은 조금 까다로워집니다. 먼저 행렬 곱셈을 설정하기 위해서는 아래 이미지와 같이 이전 행렬의 열 개수와 두 번째 행렬의 행 개수가 같아야 합니다. 이것은 곱셈을 허용하고 그 부분은 “왜?” 행렬 곱셈의 정의가 정확히 같아서 답이 없네요… 아래 그림과 같이 행렬 곱셈을 하면 선이 나타납니다.

그러나 m행 k열의 행렬과 k행 n열의 행렬을 곱하면 m행 n열의 행렬이 됩니다. 이제 행렬 곱셈 과정을 살펴보겠습니다.

이전 행렬의 행 방향 성분과 뒤 행렬의 열 방향 성분이 차례로 곱해지고 더해지는 것을 볼 수 있습니다. 이 행렬 곱셈 과정에서 각 행렬의 행과 열의 수는 위에서 언급한 바와 같이 일치해야 합니다. 이 경우 각각의 2×2 행렬이 곱해지기 때문에 결과도 2×2 행렬이 된다.
“따라서 행렬 곱셈은 가환적이지 않습니다.”
절대 헷갈리지 말자. 행렬 곱셈 연산을 수행할 때 실수로 교환 속성을 사용하려고 할 수 있습니다. 조심하세요.
4. 시행
이제 행렬과 기본 연산이 무엇인지 알았으므로 C++ 소스 코드에서 배운 모든 것을 구현할 것입니다.
Matrix.h
#ifndef __MATRIX_H__
#define __MATRIX_H__
#include <initializer_list>
#define DEFAULT_EPSILON 0.000001f
class Matrix
{
public:
Matrix(const Matrix& matrix);
Matrix(size_t rowNum, size_t columnNum);
Matrix(std::initializer_list<std::initializer_list<float>> matrix);
~Matrix();
public:
size_t GetRowNum() const;
size_t GetColumnNum() const;
void SetEpsilon(float epsilon);
float GetEpsilon() const;
void GetDiagonalElements(float diagonalElements()) const;
Matrix GetTransposeMatrix() const;
bool IsZeroMatrix() const;
bool IsSymmetricMatrix() const;
bool IsSkewSymmetricMatrix() const;
bool IsSquareMatrix() const;
bool IsDiagonalMatrix() const;
bool IsIdentityMatrix() const;
public:
Matrix& operator=(const Matrix& matrix);
Matrix operator+(const Matrix& matrix) const;
Matrix operator-(const Matrix& matrix) const;
Matrix operator*(const Matrix& matrix) const;
Matrix operator*(float value) const;
friend Matrix operator*(float value, const Matrix& matrix);
Matrix& operator+=(const Matrix& matrix);
Matrix& operator-=(const Matrix& matrix);
Matrix& operator*=(const Matrix& matrix);
Matrix& operator*=(float value);
float* operator()(int i) const;
private:
size_t rowNum;
size_t columnNum;
float** elements;
float epsilon;
};
#endif
매트릭스.cpp
#include "Matrix.h"
#include <cmath>
#include <cassert>
Matrix::Matrix(const Matrix& matrix)
: epsilon(DEFAULT_EPSILON)
{
rowNum = matrix.rowNum;
columnNum = matrix.columnNum;
elements = new float*(rowNum);
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
elements(i) = new float(columnNum);
for (j = 0; j < columnNum; ++j)
{
elements(i)(j) = matrix(i)(j);
}
}
}
Matrix::Matrix(size_t rowNum, size_t columnNum)
: epsilon(DEFAULT_EPSILON)
, rowNum(rowNum)
, columnNum(columnNum)
{
elements = new float*(rowNum);
for (int i = 0; i < rowNum; ++i)
{
elements(i) = new float(columnNum) { 0.0f };
}
}
Matrix::Matrix(std::initializer_list<std::initializer_list<float>> matrix)
: epsilon(DEFAULT_EPSILON)
{
rowNum = matrix.size();
columnNum = matrix.begin()->size();
elements = new float*(rowNum);
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
elements(i) = new float(columnNum);
for (j = 0; j < columnNum; ++j)
{
elements(i)(j) = matrix.begin()(i).begin()(j);
}
}
}
Matrix::~Matrix()
{
for (int i = 0; i < rowNum; ++i)
{
delete() elements(i);
}
delete() elements;
}
size_t Matrix::GetRowNum() const
{
return rowNum;
}
size_t Matrix::GetColumnNum() const
{
return columnNum;
}
void Matrix::SetEpsilon(float epsilon)
{
this->epsilon = epsilon;
}
float Matrix::GetEpsilon() const
{
return epsilon;
}
void Matrix::GetDiagonalElements(float diagonalElements()) const
{
int min = rowNum < columnNum ? rowNum : columnNum;
for (int i = 0; i < min; ++i)
{
diagonalElements(i) = elements(i)(i);
}
}
Matrix Matrix::GetTransposeMatrix() const
{
Matrix matrix(columnNum, rowNum);
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
matrix(j)(i) = elements(i)(j);
}
}
return matrix;
}
bool Matrix::IsZeroMatrix() const
{
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
if (fabs(elements(i)(j)) > epsilon)
{
return false;
}
}
}
return true;
}
bool Matrix::IsSymmetricMatrix() const
{
if (!IsSquareMatrix())
{
return false;
}
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = i + 1; j < columnNum; ++j)
{
if (fabs(elements(i)(j) - elements(j)(i)) > epsilon)
{
return false;
}
}
}
return true;
}
bool Matrix::IsSkewSymmetricMatrix() const
{
if (!IsSquareMatrix())
{
return false;
}
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = i + 1; j < columnNum; ++j)
{
if (fabs(elements(i)(j) + elements(j)(i)) > epsilon)
{
return false;
}
}
}
return true;
}
bool Matrix::IsSquareMatrix() const
{
return rowNum == columnNum;
}
bool Matrix::IsDiagonalMatrix() const
{
if (!IsSquareMatrix())
{
return false;
}
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
if (fabs(elements(i)(j)) > epsilon && i != j)
{
return false;
}
}
}
return true;
}
bool Matrix::IsIdentityMatrix() const
{
if (!IsDiagonalMatrix())
{
return false;
}
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
if (fabs(elements(i)(j) - 1.0f) > epsilon)
{
return false;
}
}
}
return true;
}
Matrix& Matrix::operator=(const Matrix& matrix)
{
assert(rowNum == matrix.rowNum && columnNum == matrix.columnNum, "Cannot perform operation due to different sizes of matrices.");
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
elements(i)(j) = matrix(i)(j);
}
}
return *this;
}
Matrix Matrix::operator+(const Matrix& matrix) const
{
assert(rowNum == matrix.rowNum && columnNum == matrix.columnNum, "Cannot perform operation due to different sizes of matrices.");
Matrix ret = *this;
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
ret.elements(i)(j) += matrix.elements(i)(j);
}
}
return ret;
}
Matrix Matrix::operator-(const Matrix& matrix) const
{
assert(rowNum == matrix.rowNum && columnNum == matrix.columnNum, "Cannot perform operation due to different sizes of matrices.");
Matrix ret = *this;
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
ret.elements(i)(j) -= matrix.elements(i)(j);
}
}
return ret;
}
Matrix Matrix::operator*(const Matrix& matrix) const
{
assert(columnNum == matrix.rowNum, "Matrix multiplication does not satisfy the necessary conditions.");
Matrix ret(rowNum, matrix.columnNum);
int i;
int j;
int k;
int curRow = 0;
int curColumn = 0;
for (i = 0; i < rowNum; ++i)
{
curColumn = 0;
for (j = 0; j < matrix.columnNum; ++j)
{
for (k = 0; k < columnNum; ++k)
{
ret(curRow)(curColumn) += (elements(curRow)(k) * matrix(k)(curColumn));
}
++curColumn;
}
++curRow;
}
return ret;
}
Matrix Matrix::operator*(float value) const
{
Matrix ret = *this;
int i;
int j;
for (i = 0; i < rowNum; ++i)
{
for (j = 0; j < columnNum; ++j)
{
ret.elements(i)(j) *= value;
}
}
return ret;
}
Matrix operator*(float value, const Matrix& matrix)
{
Matrix ret = matrix;
int i;
int j;
for (i = 0; i < ret.GetRowNum(); ++i)
{
for (j = 0; j < ret.GetColumnNum(); ++j)
{
ret.elements(i)(j) *= value;
}
}
return ret;
}
Matrix& Matrix::operator+=(const Matrix& matrix)
{
*this = *this + matrix;
return *this;
}
Matrix& Matrix::operator-=(const Matrix& matrix)
{
*this = *this - matrix;
return *this;
}
Matrix& Matrix::operator*=(const Matrix& matrix)
{
*this = *this * matrix;
return *this;
}
Matrix& Matrix::operator*=(float value)
{
*this = *this * value;
return *this;
}
float* Matrix::operator()(int i) const
{
assert(i < rowNum, "Out of range.");
return elements(i);
}